La Pierre qui Chante - Géométrie Sacrée: septembre 2015

La Pierre qui Chante

Géométrie Sacrée aux Roches de Marlin

 

 

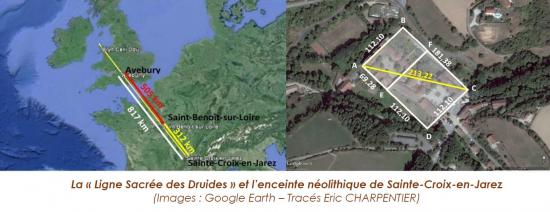
Dans un récent article¹ intitulé « La ligne sacrée des Druides », je mettais en évidence l’importance du site mégalithique des Roches de Marlin et cela dans une dimension qui dépasse l’entendement.  Associé au site de la chartreuse de Sainte-Croix-en-Jarez, celui des Roches de Marlin se rattache aux plus grands lieux sacrés du druidisme de l’époque celte : Bryn Celli Ddu sur l’île de Mona au Pays de Galles, Avebury en Angleterre, la Forêt des Carnutes en France et Sainte-Croix/Marlin se positionnent parfaitement sur une même ligne tout en se faisant écho selon la Divine Proportion du Nombre d’Or.

Nous avions également montré qu’à l’emplacement même de la chartreuse du Pilat, se tenait il y a environ 4000 ans une vaste enceinte néolithique de forme rectangulaire, elle aussi aux proportions du Nombre d’Or.

 

 

Ce Nombre d’Or est l’élément primordial à toute géométrie sacrée car il incarne la Perfection et l’Harmonie naturelle. Nous aborderons ici une infime partie de cette géométrie sacrée appliquée exclusivement au site de Sainte-Croix/Marlin en nous concentrant uniquement sur l’élément phare de ce lieu, à savoir la fameuse Pierre qui Chante des Roches de Marlin.

La Pierre qui Chante et les Roches de Marlin

La Pierre qui Chante des Roches de Marlin, autrement appelée la Pierre du Diable, est sans conteste la star mégalithique du Pilat. Jusque dans les années 1960, elle n’était connue que des habitants des environs et n’avait jamais fait l’objet de compte rendu par les archéologues du XIX^ème siècle. Nous devons la découverte de cette pierre – en tous les cas pour le grand public -  à André Douzet qui fut le premier à écrire sur le sujet dans son livre « Mystérieux Pilat mégalithique et médiéval », édité en 1983.

 

 

Nulle autre roche que la Pierre qui Chante ne possède, dans les monts du Pilat, autant de légendes associées à elle : Il y a tout d’abord celle du chevalier volant la perle (la pierre ?) au Dragon ; puis celle qui raconte que quiconque s’endort sur la pierre se réveille soit avec la connaissance universelle, soit en ayant perdu la raison ; ou encore celle du Diable, la plus connue sans doute, lequel ramenant sur son dos cette roche du Dauphiné et n’en pouvant plus de la porter, fini enfin par la déposer sur le site des Roches de Marlin ; et bien d’autres histoires  encore de notre folklore régional …etc.

Le site des Roches de Marlin compte une trentaine de roches à cupules ou bassins dont nous avons dressé l’inventaire² sur les pages du site Nature et Mystère. Mais parmi elles, quelques-unes seulement et toutes en forme d’amande, semblent avoir été posées et orientées par l’Homme. La Pierre qui Chante étant la plus remarquable d’entre elles a suscité les intérêts les plus diverses : chercheurs en tous genres, amateurs d’ésotérisme, néo-druidisme, radiesthésistes, géobiologues, archéologues, historiens, …etc.

Nos travaux sur ce site ont montré que chacune de ces pierres posées, l’avaient été selon une géométrie bien précise utilisant des formes sacrées comme le Bicarré, le rectangle d’or, le carré, …etc. Cette géométrie s’inscrit comme principe fondamental d’une science mégalithique que nous avons aujourd’hui totalement oubliée. Le spécialiste du mégalithisme anglo-saxon Howard Crowhurst qui œuvre sur le sujet depuis des décennies, a mis en évidence qu’une même expression géométrique existait dans tous les plus grands sites mégalithiques du monde. De notre côté, c’est en voulant appliquer ces principes fondamentaux aux Roches de Marlin que nous y avons découvert toute une face cachée de cette pensée des bâtisseurs de mégalithes.

 

Amorce d’une géométrie sacrée

 

La Pierre qui Chante est donc une roche posée comme en équilibre sur l’affleurement rocheux de la crête de Marlin. Cette pierre remarquable de forme oblongue ou plutôt de type « amande »  mesure 4,22 m de longueur par 1,60 m de largeur dans ses plus grandes dimensions. Elle est inclinée de 20-25° par rapport à l’horizontal et est orientée à 30° d’azimut nord.  Elle porte trois bassins d’une vingtaine de centimètres de diamètre pour le plus grand, lesquels dessinent sur la roche la forme d’un visage qui semble chanter et qui a probablement contribué à donner son nom à cette pierre. Elle se situe entre la pierre du  Dauphin et le rocher de la Proue que nous allons brièvement décrire.

La pierre du Dauphin est en quelque sorte la sœur jumelle de la Pierre qui Chante. Bien que plus petite (3,00 m x 1,62 m), il s’agit aussi d’une pierre posée comme en équilibre, de forme oblongue ou en amande avec pour sa part un seul bassin circulaire. Elle est inclinée d’environ 15° par rapport à l’horizontale et orientée à 110° d’azimut nord. Elle se situe à environ 60 mètres à l’est de la Pierre qui Chante. On lui attribue le nom de Dauphin du fait que de profil, elle prend l’allure de ce mammifère marin.

Le rocher de la Proue est quant à lui l’une des roches les plus imposantes du site où il occupe l’extrémité ouest. Il s’agit de la roche la plus en vue de la partie occidentale de la Crête de Marlin au point qu’on la distingue nettement des collines voisines. Il ne s’agit pas là d’une roche posée par l’homme mais d’un vaste rocher naturel d’une douzaine de mètres de longueur orienté est-ouest.

La particularité de cette roche est de posséder quelques petites cupules mais surtout un grand bassin en forme de cuve cylindrique de 40 à 50 cm de diamètre dont le centre est distant de 56 mètres à l’ouest de la Pierre qui Chante.

 

 

Lorsque l’on examine le site de Marlin en imagerie aérienne, les trois roches que nous venons de présenter semblent à la fois être équidistantes et alignées. En fait, à y regarder de plus près ce n’est pas tout à fait le cas. La distance séparant le centre de la Pierre qui Chante et le centre du bassin de la Proue est de 56 mètres alors que celle séparant les centres de la Pierre qui Chante et du Dauphin est de 60 mètres. De même l’alignement formé par les centres de la Pierre qui Chante et celui du bassin de la Proue est parfaitement orientée Est-Ouest, c’est-à-dire 90° azimut nord et on voit bien que la pierre du Dauphin est décalée de cet axe d’un plus de 6m vers le sud.

La relation à prendre en compte ici est donc bien celle qui lie la Pierre qui Chante au rocher de la Proue : d’une part la distance séparant le centre du grand bassin de la Proue au centre de la Pierre qui Chante est équivalente à 56 mètres qui est ni plus ni moins, la mesure mégalithique utilisée sur ce site ;  mais d’autre part, l’orientation donnée par l’alignement de ces deux roches donne la direction cardinale exacte Est – Ouest.

 

 

Il n’est pas à propos ici de s’attarder sur la distance de 56 mètres qui comme nous venons de le dire est la mesure utilisée sur l’ensemble du site Sainte-Croix / Marlin. Disons simplement que cette mesure a été retenue par les bâtisseurs de mégalithes car il s’agit précisément de celle qu’il convenait d’utiliser en ce lieu sacré : c’est une mesure qui une fois encore est en pleine relation avec le Nombre d’Or.

L’orientation Est-Ouest donnée par l’alignement des deux roches est quant à elle révélatrice d’une volonté manifeste de marquer les axes cardinaux. Nous verrons plus loin comment la Pierre qui Chante détermine encore l’axe Nord-Sud parfait.

L’axe Est-Ouest est aussi l’axe des équinoxes, c’est-à-dire la direction dans laquelle le soleil va se lever aux jours qui déterminent encore aujourd’hui le début des saisons du printemps (20 - 21 mars) et de l’automne (20 - 23 septembre). Il s’agit là encore ni plus ni moins des deux jours de l’année où la durée du jour est égale à la durée de la nuit. Nous laisserons encore de côté ici, la portée symbolique que pouvait avoir cette orientation pour les bâtisseurs du néolithique…

Dans la courte description de la Pierre qui Chante que nous avons faite au début de ce chapitre, nous avons signalé que son azimut était de 30° Nord. C’est-à-dire que la pierre est orientée de 30° exactement par rapport au nord géographique qui définit l’axe de rotation de notre planète. Patrick Berlier dans sa brochure sur les Roches de Merlin donne un azimut de 40° à la Pierre qui Chante, ce qui n’a pas manqué de nous surprendre. En fait, l’azimut de 40° est certainement celui donné par une boussole magnétique, indiquant en principe le nord magnétique et non le nord géographique. Mais l’écart de 10° est trop important pour résulter de la seule déclinaison magnétique et probablement devons-nous considérer qu’une boussole magnétique peut être particulièrement perturbée au-dessus d’une roche telle que la Pierre qui Chante. Nous savons par les géobiologues tels que Jacques Bonvin³ ou Adolphe Landspurg⁴ que le site des Roches de Marlin tient une place particulière parmi les Hauts Lieux d’énergie en France. Jacques Bonvin allant même jusqu’à admettre que ce qu’il détecte ici n’a rien de commun : « En effet, selon nos schémas habituels, il n’existe sur ce lieu, ni énergie tellurique, ni énergie cosmique, mais autre chose d’indéfinissable et dangereux ».

L’orientation de la Pierre qui Chante est donc exactement 30° azimut nord ce qui là encore n’est pas anodin et montre que les directions cardinales étaient parfaitement connues des bâtisseurs de mégalithes. Symboliquement, rappelons que 30° est la douzième partie du cercle et que cette division du cercle en 360° entretient un rapport évident avec l’année solaire de 365 jours. L’orientation géométrique 30° pourrait donc renvoyer à la notion de division de l’année solaire en 12 mois.

Par ces premiers éléments de constat, nous voyons ici l’amorce de principes utilisés en géométrie sacrée à l’époque des bâtisseurs de mégalithes tels que les a définis Howard Crowhurst : connaissance des axes cardinaux (Nord-Sud et Est-Ouest), connaissance de mesures sacrées (56 m et Nombre d’Or), connaissances astrales et calendaires (solstices / équinoxes, année solaire).

Nous allons maintenant mettre en application cette géométrie sacrée et voir comment la Pierre qui Chante s’inscrit dans cet ensemble. Mais avant cela, quelques notions relatives au Nombre d’Or permettront de mieux comprendre certains aspects de cette géométrie.

 

Phi : Le Nombre d’Or

 

Le Nombre d’Or ? (Phi) du nom de Phidias, l’architecte Grec ayant construit le Parthénon sur l’Acropole d’Athènes vers 460 av. J.-C., est certainement le nombre qui compose l’Univers entier. Il a pour valeur numérique 1,618… ([?5+1]/2), possède des caractéristiques mathématiques uniques, il est considéré comme donnant la proportion harmonique parfaite, appelée encore la Divine Proportion, que l’on retrouve dans tout ce qui constitue la vie sur Terre (les végétaux, le corps humain, …) et qui fut largement utilisée dans tous les arts figuratifs comme la Peinture, la Sculpture ou l’Architecture comme symbole du Sacré et de la Perfection.

La chartreuse de Sainte-Croix-en-Jarez elle-même ne déroge pas à cette règle puisqu’elle est entièrement construite sur les bases du Nombre d’Or. Mieux encore, si nous savions déjà que la Grande Pyramide de Khéops en Egypte était également construite sur la notion du Nombre d’Or, de récents travaux menés par Howard Crowhurst ont également démontré que la Divine Proportion et le Nombre d’Or sont tout aussi présents dans le mégalithisme anglais comme à Stanton Drew par exemple.

 

 

 

Géométrie et Nombre d’Or

 

Pour les bâtisseurs de l’époque néolithique, le nombre d’or ne pouvait s’appréhender que par la géométrie : l’arithmétique ([?5+1]/2) et les nombres décimaux 1,618… leur étant totalement inconnu.

Deux constructions géométriques permettent d’obtenir simplement la Divine Proportion :

• Le Bicarré ou réunion de deux carrés
• La Mandorle ou amande maçonnique

 

1. Le Bicarré.

De toutes les formes géométriques de base, le Bicarré est certainement la plus utilisée en architecture sacrée. Elle est présente dans la Grande Pyramide de Khéops en Egypte, dans le temple de Salomon, dans les alignements de Carnac, …etc. Les bâtisseurs des églises romanes et gothiques utilisaient le Bicarré dans le tracé régulateur de ces édifices et ils attribuaient à chacun des quatre sommets du Bicarré les quatre éléments majeurs que sont l’Eau, l’Air, la Terre et le Feu.

Plus proche de nous, le Bicarré a été largement utilisé sur le site mégalithique de Sainte-Croix / Marlin : il donne par exemple l’orientation du solstice d’été à Sainte-Croix, où encore relie le Champ du Peu à la roche du Châtaigner, la roche de la Proue à la roche du Châtaigner, …etc.

Le Bicarré permet la construction géométrique de la Divine Proportion selon le schéma ci-dessous.

 

 

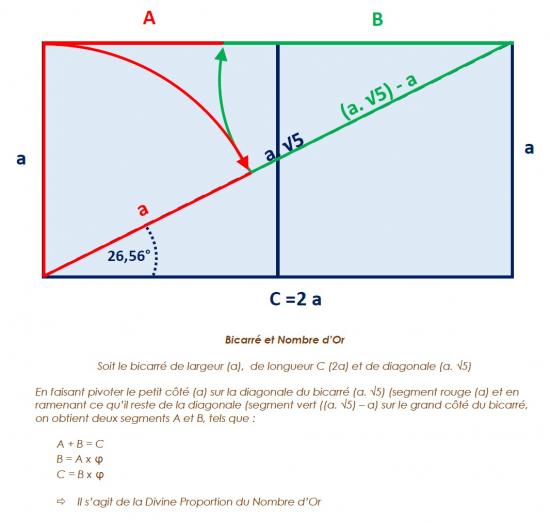
En adoptant la valeur 1 pour unité de petit côté, cette figure exprime par la diagonale d’un des deux carrés composant le Bicarré, la racine carrée de deux √2, ainsi que par la diagonale du Bicarré la racine carrée de cinq √5 qui sont toutes deux des valeurs numériques irrationnelles pouvant facilement être obtenue à partir du Bicarré ayant 1 pour unité.

De plus, le triangle rectangle formé par les côtés et la diagonale de ce Bicarré aurait pour périmètre P = 1 + 2 + ?5 = 5,236, c’est-à-dire la mesure de 10 coudées royales égyptiennes (1CRE = 52,36 cm). Or nous savons aussi que 5 coudées royales égyptiennes valent le nombre d’or au carré, soit ?² = ? + 1 = 5 x 0,5236 = 2,618… Nous voyons là que le Bicarré entretient des relations très particulières avec le Nombre d’Or  ? et que celles-ci furent très habilement utilisées sous l’Egypte Ancienne.

 

2 – La Mandorle

 

Egalement appelée Amande dans la Tradition maçonnique, la Mandorle est la forme générée géométriquement par l’intersection de deux cercles. Cette construction qui peut paraître des plus banales est pourtant à la base de toutes les autres puisque c’est la seule qui permette d’obtenir l’angle droit ! Symboliquement parlant, elle précède donc le Bicarré qui est une construction rectangulaire…

De plus, en ayant 1 pour unité de petit axe (c’est aussi le rayon des deux cercles), la Mandorle ainsi créée va permettre d’obtenir très facilement le Nombre d’Or et la Divine Proportion selon le schéma ci-dessous.

 

 

 

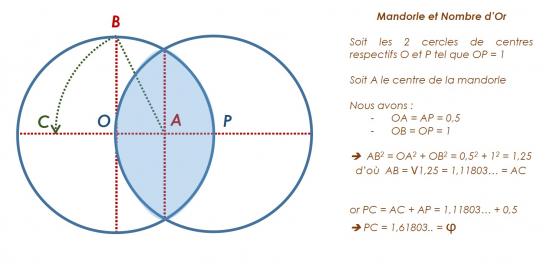
Outre la construction géométrique du Nombre d’Or ?, cette figure permet encore d’obtenir très facilement la forme géométrique d’un Rectangle d’Or, ainsi que la valeur géométrique du Nombre d’Or au carré ?², ou encore la racine carrée du Nombre d’Or √?, mais là n’est pas l’objet de cette démonstration.

Une autre particularité de cette Mandorle ayant pour petit axe la valeur 1, c’est-à-dire des cercles de rayon 1, est d’exprimer, cette fois-ci par son grand axe, la valeur irrationnelle du nombre racine carrée de trois √3. Nous avons vu avec le Bicarré ci-dessus qu’un carré ayant 1 pour unité de côté exprime √2 par sa diagonale et qu’un Bicarré ayant 1 pour unité de petit côté exprime √5 par sa diagonale. Avec la construction de la Mandorle et l’expression géométrique du nombre irrationnel √3 par son grand axe, nous voyons que les racines carrées des premiers nombres entiers 1, 2, 3, 4, 5 étaient facilement accessibles aux bâtisseurs de mégalithes par la géométrie (en rappelant que √1=1 et √4=2).

Nous verrons plus bas comment l’application de ces racines carrées fut utilisée sur le site des Roches de Marlin.

 

La Pierre qui Chante et le Nombre d’Or

 

La forme en amande de la Pierre qui Chante est typique des pierres posées du site de Marlin et n’est pas sans rappeler celle de la Mandorle qui permet précisément d’obtenir le Nombre d’Or par la géométrie. Devons-nous alors considérer que la forme en amande de ces pierres était précisément recherchée par les bâtisseurs du site de Marlin pour évoquer le Nombre d’or ? D’aucuns rétorqueront que la forme en amande de ces pierres posées résulte simplement du phénomène naturel de délitage de ce type de roches qu’est le schiste.

Et ils auront probablement raison ! Le schiste est une roche qui a pour particularité d'avoir un aspect feuilleté et de se débiter en plaques fines ou « feuillet rocheux ». Ce phénomène naturel s’entend à toutes les échelles possibles : du plus petit caillou aux dimensions plus importantes comme celles de la Pierre qui Chante. Nous avons pu nous-même constater ce phénomène en trouvant dans l’interstice d’une fissure du rocher de la Proue un petit éclat de roche schisteux de quelques centimètres de longueur ayant précisément la forme d’une amande.

 

 

En admettant que les bâtisseurs du site de Marlin maîtrisaient la géométrie du Nombre d’Or, il est fort possible que les caractéristiques naturelles des pierres de schistes se délitant en amandes aient été recherchées comme symbole de la Mandorle. Les pierres en amande auraient alors portées en elles dès l’origine une symbolique exprimant l’harmonie opérée par le Nombre d’Or. Il est à noter encore que cette forme en amande est aussi celle qui résulte de la taille des silex telle que la pratiquait les hommes de la préhistoire.

Mais la forme en amande de la Pierre qui Chante n’est pas le seul élément qui peut la relier à la géométrie du Nombre d’Or. Ce qui certainement place cette pierre à un niveau supérieur aux autres roches du site de Marlin, ce sont ses dimensions : en effet si l’on mesure les deux axes les plus longs de la pierre on s’aperçoit qu’elle mesure 1,60 m de largeur par 4,22 m de longueur. Or 1,60 m est une mesure très proche de celle du Nombre d’Or 1,618 et 4,22 m correspond au centimètre près à la valeur du Nombre d’Or élevé à la puissance trois : ?³ = 4,23.

 

 

Nous pourrions encore nous interroger sur la construction géométrique permettant d’obtenir une amande ayant les caractéristiques de la Pierre qui Chante. Les équations mathématiques montrent que le rayon des cercles à construire pour obtenir une Mandorle ayant ? pour petit axe et ?³ pour grand axe, doit avoir pour valeur R = 3,177… [(3/2) ? + ¾].

Il est encore intéressant ici de constater que cette valeur numérique est très proche de celle donnant l’angle d’un Rectangle d’Or : 31,72°, rectangle qui se construit facilement à partir de la Mandorle vue plus haut.

 

 

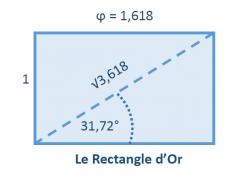
Nous pourrions raisonnablement penser qu’une heureuse coïncidence a donné ces dimensions à cette amande remarquable. Mais l’expression du Nombre d’Or se retrouvant à maintes reprises dans la géométrie sacrée de ce sanctuaire néolithique, nous ne pouvons nous résoudre à y voir une quelconque part de hasard.

D’autant qu’un autre constat va encore nous surprendre : il s’agit du rapport existant entre les dimensions des différentes pierres posées du site de Marlin. En présentant plus haut la pierre du Dauphin, nous avons signalé que les dimensions de cette amande étaient de 3,00 m x 1,62 m. Outre la largeur qui est la même que sa sœur jumelle et qui exprime à nouveau le Nombre d’Or 1,618… nous constatons que le rapport des longueurs de ces deux roches 4,23 / 3,00 = 1,412… qui est en soit une valeur très proche de celle de √2 = 1,414… et comme ce constat se voit confirmé par un rapport similaire (1,4) existant entre la pierre du Dauphin et une troisième roche posée que nous appelons l’ « Amande », là encore nous avons du mal à y voir une quelconque part de hasard.

 

La Pierre qui Chante dans la géométrie sacrée des Roches de Marlin.

 

Dans son ouvrage sur la Troménie de Locronan⁵, Howard Crowhurst fait la démonstration nette et précise, que toutes les stations de la procession sont positionnées selon une géométrie qui ne doit rien au hasard. Il ressort de ses travaux, que la fameuse Pierre Sacrée des Druides (Ar Gazeck ou Kazeg Ven, c’est-à-dire la Jument de Pierre) située sur le parcours de la grande troménie intervient dans le positionnement des stations comme une véritable pierre angulaire : celle à partir de laquelle toutes les autres sont disposées. Il relève notamment à titre d’exemple que les stations 1, 2 et 3 de la troménie sont fixées par les diagonales d’un Tricarré, d’un Bicarré et d’un Rectangle d’Or, trois rectangles bien particuliers utilisés en géométrie sacrée et dont les diagonales relient chacune de ces trois stations à la pierre angulaire, la Pierre Sacrée des Druides.

Or il s’avère que le même principe constructif existe sur le site des Roches de Marlin pour lequel la roche du Châtaigner va jouer le même rôle de pierre angulaire que la Kazeg Ven à Locronan.

La Roche du Châtaigner qui ferme le site mégalithique de Marlin sur sa partie Nord est un peu moins connue que ses consœurs de la crête de Marlin car elle se situe franchement à l’écart du groupe principal. Eloignée d’environ un kilomètre par le chemin qui monte à la crête depuis le hameau de Marlin, nous lui avons conservé le nom qu’elle portait au XVIII^ème siècle bien que Patrick Berlier la nomme la roche en « U » dans sa plaquette consacrée aux Roches de Merlin. Cette roche semble en fait constituée de trois pierres un peu en forme de fer à cheval qui n’est pas sans rappeler d’ailleurs les trois pierres du Cove de Stanton Drew ou les trois trilithes de Stonehenge en Angleterre.

Il s’agit sans doute du gardien du site dont parle Jacques Bonvin dans son livre : « cette pierre (la Pierre qui Chante) est extrêmement protégée. Il existe près de trois gardiens du seuil qui veillent et qui sont attentifs aux visiteurs, au moins un kilomètre avant d’arriver près d’elle ».

 

 

Nous avions déjà évoqué la roche du Châtaigner dans la « Ligne sacrée des Druides » en montrant qu’elle reliait l’un des angles de l’enceinte néolithique de Sainte-Croix-en-Jarez par un Tricarré, ou encore le Champ du Peu par un Bicarré, mais là ne sont pas ses seules caractéristiques.

 

 

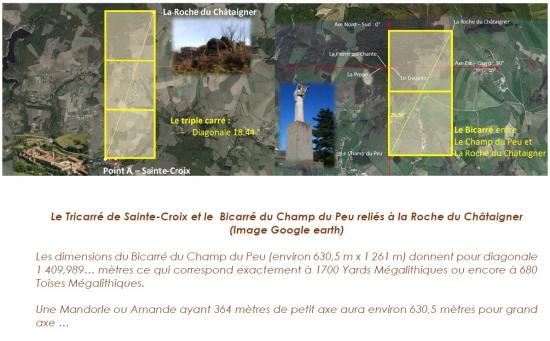
Sans entrer ici dans les détails de chacune des roches composant le site mégalithique, signalons simplement à titre d’exemple que la roche du Châtaigner positionne entre autres :

- le rocher de la Proue selon un Bicarré d’unité 364 mètres,

- la pierre du Dauphin selon un rectangle d’or d’unité 370 mètres environ

- la pierre des Loives selon un rectangle 5/2 d’unité 364 mètres à nouveau.

 

En fait, on s’aperçoit vite que tous les points majeurs du site de Sainte-Croix / Marlin entretiennent une relation géométrique avec cette pierre angulaire qu’est la roche du Châtaigner et que cette relation géométrique se traduit dans tous les cas par un rectangle sacré(Bicarré, Tricarré ou Rectangle d’Or) ou un rectangle Parfait (Carré) lesquels orientés selon les axes cardinaux, voient leurs diagonales respectives relier chacun de ces points majeurs à la roche du Châtaigner.

La Pierre qui Chante quant à elle, tient une place toute particulière parmi ces points majeurs du site mégalithique car le lien qu’elle entretient avec la pierre angulaire diffère géométriquement et symboliquement parlant des autres formes constatées : ici, ni carré, ni rectangle… mais le triangle. En effet, la ligne reliant la Pierre qui Chante à la roche du Châtaigner est orientée exactement à 60° azimut nord  ce qui correspond à l’angle géométrique exact d’un triangle équilatéral.

 

 

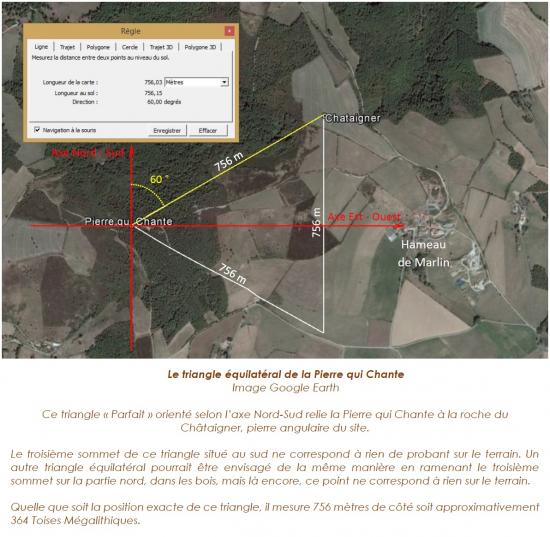
La mesure obtenue pour le côté de ce triangle « Parfait » est d’environ 756 mètres, nombre qui n’est pas sans rappeler celui, qui dans le système de mesure britannique, donne pour dimension de la base de la Grande Pyramide de Khéops en Egypte  la mesure de 756 pieds anglais (440 coudées royales égyptiennes de 52,36 cm).

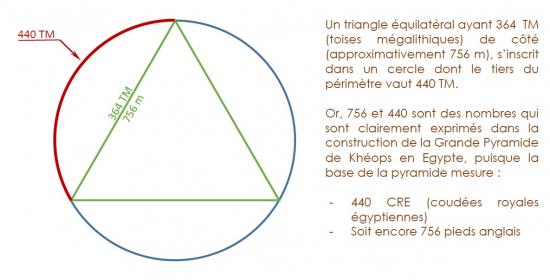
Mais le plus surprenant est le rapport qu’il semble y avoir entre cette mesure de 756 mètres et une autre unité de mesure dite Toise Mégalithique qui fut largement utilisée dans les sites de Grand Bretagne ainsi qu’à Carnac en France :   en effet, 756 mètres sont aussi approximativement 364 Toises Mégalithiques : 1 TM = 2,5 Yards Mégalithiques et 1 YM = 0,8294 mètres (la mesure exacte de  364 TM donnerait mathématiquement pour côté théorique du triangle équilatéral le nombre amusant de 364 x 2,5 x 0,8294 = 754,754 mètres, soit une erreur de 1,6 ‰ avec notre mesure de 756 mètres)

Notons enfin  l’importance du nombre 364 exprimé au moins à quatre reprises : trois fois dans les liens unissant la roche du Châtaigner avec celle de la Proue, puis celle des Loives et enfin avec la Pierre qui Chante ; et une quatrième fois, le nombre 364 est exprimé implicitement dans le Bicarré (630,5 m x 1261 m ) qui relie le Champ du Peu à la roche du Châtaigner, puisque 630,5 = 364 x √3 et qu’il s’agit là du rapport existant entre le grand axe et le petit axe d’une Mandorle !

Ce nombre 364 qui associe d’une part deux nombres lunaires : 13 lunaisons de 28 jours et d’autre part deux nombres calendaires : 52 semaines de 7 jours s’approche trop du nombre déterminant l’année solaire exacte de 365 jours, pour laisser une part de hasard dans le choix de cette mesure.

Il semblerait en outre, mais ce point mériterait d’être confirmé par des personnes plus compétentes que nous en matière de métrologie, que ce nombre 364, exprimé dans la géométrie du triangle équilatéral de la Pierre qui Chante, mette en résonnance notre système métrique avec les systèmes de mesure britannique (pied anglais), mégalithique (toise mégalithique) et égyptien (coudée royale égyptienne). La construction géométrique ci-dessous illustre ce constat.

 

 

Eric CHARPENTIER

A Saint-Sorlin, le 10 septembre 2015

 

Notes :

1 - En ligne sur http://regardsdupilat.free.fr/ et http://ulyne.e-monsite.com

2 - http://ulyne.e-monsite.com/pages/content/rhone/longes.html

3 - Jacques Bonvin, « Mégalithes – Lieux d’énergie », éd. Mosaïque, 2007

4 - Adolphe Landspurg, « Les Hauts Lieux d’énergie en France », éd. Dangles, 2006

5 - Howard Crowhurst, « Les origines secrètes de la Troménie de Locronan », Epistemea,  2013